State Estimation

Revise

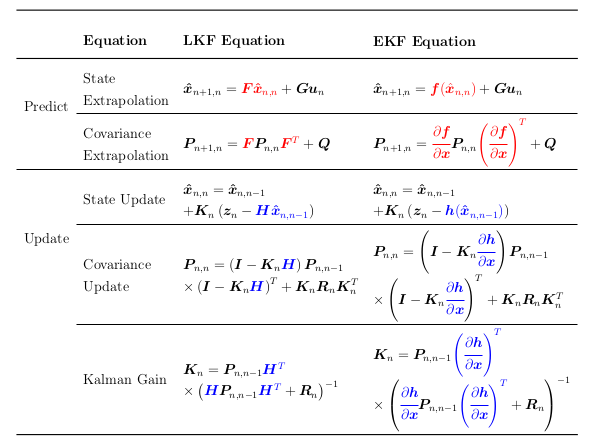
Extended Kalman Filter

Unlike the Kalman Filter and the Multivariate Kalman Filter, most real-life systems are non-linear. Understanding the linear Kalman Filter will help to understand how the EKF works.

To handle non-linear systems, the EKF uses linear approximation techniques in which it performs analytic linearization of the model at each point in time.

Modifications for non-linear systems are sub-optimal due to using approximated models.

For a linear system, the measurement equation is in the form $z_n=\mathbf{H}{x}_n$ but in a non-linear system, in this case, is $z_n=\mathbf{h}(x_n)$.

Essential Background

• Derivatives
• Partial Derivatives
• The Jacobian

Multivariate Uncertainty Projection

$${\mathbf{P}}_{out}=\frac{\partial f}{\partial x}{\mathbf{P}}_{in}{\left(\frac{\partial f}{\partial x}\right)}^T$$

• ${\mathbf{P}}_{in}$ is an input covariance
• ${\mathbf{P}}_{out}$ is a projected covariance
• $\frac{\partial f}{\partial x}$ is a state transition matrix Jacobian

Extended Kalman Filter Equations