Multi-Agent Systems

A Comprehensive Survey of Multi-Agent Reinforcement Learning

Reading Objectives

• Identify structure of the field, its limitations, and its drawbacks.
• Gain insight on the theory and the fundamentals.
• Determine direction for future research in this field.

Most MARL algorithms are derived from a model-free algorithm called Q-Learning.

The Multi-Agent Case

Generalization of MDP to the multi-agent case is the Stochastic Game (SG).

• If ${\rho }_1=...={\rho }_n$, then all agents have the same goal and the SG is fully cooperative.
• If, for example, $n=2$ and ${\rho }_1=-{\rho }_2$, then the agents have the opposite goal and the SG is fully competitive.
• Mixed games are in between and are neither fully.

Info

Stochastic games can be static or dynamic.

Benefits

Parallel Computation and Experience Sharing

Due to the decentralized structure, the sharing of experience among agents with similar tasks causes them to learn quicker and faster.

In the case of one or more agents failing, the system can redistribute the load while also allowing for replacement agents to be added later. Makes it robust!

Limitations

Complexity

The Curse of Dimensionality applies here in the case of the exponential growth of the discrete state-action space. Recall that the space-action space is $X\times U$ where the $X$ and $U$ are the number of states and actions respectively. Therefore, if you increase the number of agents exponentially, it gets even crazier and more complex!

Specifying a Learning Goal

Danger

In fully cooperative stochastic games, the common return can be jointly maximized. In other cases, however, the agents’ returns are different and correlated, therefore, cannot be maximized independently.

Several types of goals for MARL have been explored in other works such as the stability of the agent’s learning dynamics, adaptation to the changing behaviors of other agents, or both.

See Stability and Adaptation.

Nonstationarity

Agents within this system are all learning simultaneously so each agent is faced with a moving-target learning problem in which the best policy changes as the other agents’ policies changes.

From Reinforcement Learning, recall the relationship between exploration and exploitation. In MARL, complications arise due to the presence of multiple agents. Not only does the agent explore to gather information about the environment, it also gathers information about other agents.

Too Much Exploration

Will destabilize the learning dynamics of other agents making the learning task more difficult for the exploring agent.

Coordination

Surely connected to Consensus and Cooperation in Networked Multi-Agent Systems right?

Any agent’s actions on the environment depends also on the actions taking by other agents. Therefore, the agents’ choices of actions must be mutually consistent to achieve their intended effect.

Coordination usually boils down to consistently breaking ties between equally good actions or strategies.

Although typically required in cooperative settings, it can also be useful for self-interested agents i.e. simplifying each agent’s learning task by making the effects of its actions more predictable.

Stability and Adaptation

Stability

Convergence to a stationary policy.

Convergence to equilibria is a basic stability requirement i.e. agents’ strategies should eventually converge to a coordinated equilibrium. While Nash equilibria are commonly used, there are concerns about their usefulness.

Benefits of Control Theory

Control theory can contribute in addressing issues such as stability of learning dynamics and robustness against uncertainty in observations or the other agents dynamics.

Adaptation

Ensures that performance is maintained or improved as the other agents are changing their policies.

A criterion for adaptation is rationality which is a requirement that the agent converges to a best response when the other agents remain stationary.

Alternative to rationality, no-regret is the requirement is that the agent achieves a return that is at least as good as the return of any stationary strategy. Holds for any set of strategies of the other agents and prevents the learner from being exploited by other agents.

Significance

Objective

For a MARL goal to be good, it must include both components. Since the “perfect” stability and adaptation cannot be achieved simultaneously, an algorithm should guarantee bounds on both measures.

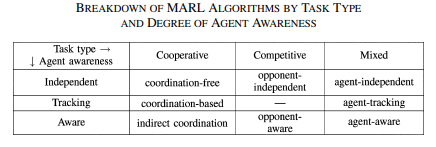
• Algorithms only focused on stability i.e. convergence, are typically unaware and independent of the other learning agents.
• Algorithms that consider adaptation to the other agents need to be aware to some extent of their behavior.

Note: If adaptation is taken to the extreme and stability is disregarded, the algorithm is only tracking the behavior of the other agents.

Algorithms

Section Outline

Section A: Fully Cooperative Tasks Section B: Explicit Coordination Mechanisms Section C: Fully Competitive Tasks Section D: Mixed Tasks

Minimax Principle

Maximize one’s benefit under the worst-case assumption that the opponent will always try to minimize it.

Game-theoretic algorithms, such as equilibrium concepts, are the strongest in the algorithms for mixed SGs

Note

Explore Win-or-Lose-Fast i.e. WoLF. In a nutshell, the agent should escape from losing situations quickly while adapting cautiously when winning to encourage convergence.

Applications

• Distributed Control
• Robotic Teams
• Automated Trading
  • Note: Seems very useful :)
• Resource Management

The Primary Concern

Practically, these algorithms are unlikely to scale-up to real-life multi-agent problems due to the large and even continuous state-action spaces.

Note: Keep in mind this was the issue at the time of publishing.

Improving Scalability

• Discovery and exploitation of the decentralized, modular structure of the multi-agent task.
• Applying domain knowledge to assist in learning solutions to realistic tasks.

Questions and Notes

• What is the Bellman Optimality Equation?
• What is the mathematical derivation to stability i.e. convergence to equilibria and why does it fall apart when tested in dynamic stochastic games?
• Although game-theoretic techniques have been used to solve dynamic multi-agent tasks but may not be the most suitable due to the dynamic nature of both the environment and behavior of the agents. So far, the game-theory-based analysis have been applied to the learning dynamics and not the actual dynamics of the environment. Has this been addressed and how?
• How much of the limitations outlined above have been resolved since 2008?
• Refer to the Markov Decision Process.